Bisogna determinare quanta strada farà il robottino RUDI per raggiungere un obiettivo a 100 metri in un numero N di segmenti utilizzando un algoritmo efficiente (nel senso che la distanza in linea d'aria di RUDI dall'obiettivo diminiusca continuamente) ma scelto in modo tale da massimizzare il percorso.
Detta L(N) la lunghezza di tale percorso in metri, sarà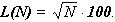
Cerchiamo il massimo della funzione al variare di α.
Detta L(N) la lunghezza di tale percorso in metri, sarà
Più in generale, detta l la distanza di RUDI dall'obiettivo, sarà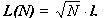 
Per la dimostrazione si faccia riferimento alla figura a fianco dove è indicato con A l'obiettivo e con BC il primo segmento del percorso.
Si può notare innanzitutto che deve essere
e 
altrimenti lungo il segmento BC il robottino si allontanerebbe dall'obiettivo.
Si può anche vedere che il percorso è massimo quando 
.
Si può notare innanzitutto che deve essere
e altrimenti lungo il segmento BC il robottino si allontanerebbe dall'obiettivo.
Si può anche vedere che il percorso è massimo quando .Dimostrerò la validità della risoluzione per induziione su N.
La relazione è banalmente valida per N=1 infatti L(1)=l.
Bisogna dimostrare che
In base alla figura abbiamo
La relazione è banalmente valida per N=1 infatti L(1)=l.
Bisogna dimostrare che
In base alla figura abbiamo
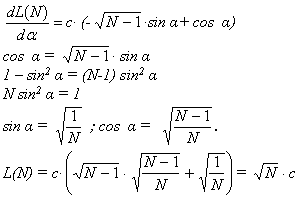
che permette di costruire l’effettivo percorso fatto da RUDI.
A questo proposito si può osservare che ogni segmento, tranne l’ultimo, può essere scelto con un angolo preso in senso orario o antiorario per cui in realtà saranno possibili 2N-1 diversi percorsi tra i quali la spirale destrorsa e sinistrorsa e l’avvicinamento a zig-zag.
Se si considera un sistema di assi coordinati con l'obiettivo sull’origine, dette (x1,y1) le coordinate della posizione del robottino, e (x2,y2) le nuove coordinate (quando si devono effettuare N passi) sarà
oppure 
Qui sotto è possibile visualizzare diversi percorsi.